IPv4 addresses have a subnet mask but instead of typing something like 255.255.255.0 we use a prefix length for IPv6. Here is an example of an IPv6 prefix:
2001:1111:2222:3333::/64
This is pretty much the same as using 192.168.1.1 /24. The number behind the / are the number of bits that we use for the prefix. In the example above it means that 2001:1111:2222:3333 is the prefix (64 bits) and everything behind it can be used for hosts.
When calculating subnets for IPv4 we can use the subnet mask to determine the network address and for IPv6 we can do something alike. For any given IPv6 address we can calculate what the prefix is but it works a bit different.
Let me show you what I’m talking about, here’s an IPv6 address that could be assigned to a host:
2001:1234:5678:1234:5678:ABCD:EF12:1234/64
What part from this IPv6 address is the prefix and what part identifies the host?

Since we use a /64 it means that the first 64 bits are the prefix. Each hexadecimal character represents 4 binary bits so that means that this part is the prefix:
2001:1234:5678:1234
This part has 16 hexadecimal characters. 16 x 4 means 64 bits. So that’s the prefix right there. The rest of the IPv6 address identifies the host:
5678:ABCD:EF12:1234
So we figured out that “2001:1234:5678:1234” is the prefix part but writing it down like this is not correct. To write down the prefix correctly we need to add zeros at the end of this prefix so that it is a 128 bit address again and add the prefix length:

2001:1234:5678:1234:0000:0000:0000:0000/64 is a valid prefix but we can shorten it. This string of zeros can be removed and replace by a single ::
2001:1234:5678:1234::/64
That’s the shortest way to write down the prefix. Let’s look at another example:
3211::1234:ABCD:5678:1010:CAFE/64
Before we can see what the prefix is, we should write down the complete address as this one has been shortened (see the :: ). Just add the zeros until we have a full 128 bit address again:
3211:0000:0000:1234:ABCD:5678:1010:CAFE/64
We still have a prefix length of 64 bits. A single hexadecimal character represents 4 binary bits, so the first 16 hexadecimal characters are the prefix:
3211:0000:0000:1234
Now we can add zeros at the end to make it a 128 bit address again and add the prefix length:
3211:0000:0000:1234::/64
That’s a good looking prefix but we can make it a little shorter:
3211:0:0:1234::/64
4 zeroes in a row can be replaced by a single one, so “3211:0:0:1234::/64” is the shortest we can make this prefix.
Depending on the prefix length it makes the calculations very easy or (very) difficult. In the examples I just showed you both prefixes had a length of 64. What if I had a prefix length of /53 or something?
Each hexadecimal character represents 4 binary bits. When your prefix length is a multiple of 16 then it’s easy to calculate because 16 binary bits represent 4 hexadecimal characters.
Here’s an illustration:
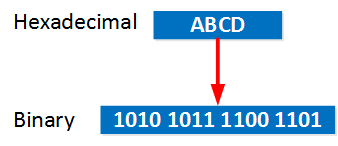
So with a prefix length of 64 we have 4 “blocks” with 4 hexadecimal characters each which makes it easy to calculate. When the prefix length is a multiple of 4 then it’s still not too bad because the boundary will be a single hexadecimal character.
When the prefix length is not a multiple of 16 or 4 it means we have to do some binary calculations. Let me give you an example!
2001:1234:abcd:5678:9877:3322:5541:aabb/53
This is our IPv6 address and I would like to know the prefix for this address. Where do I start?


very simple explanation yet so informative. thank you
The best I’ve seen on this, without straying into
geeksville and losing me.
Very simple, thank you, for the explanation
One more example would’ve been nice Very useful though
Very useful though
Hey Rene,
Could you explain how we determine where to cut off the end of the prefix? (see image attached)